Active regression

In this example, we are going to demonstrate how can the ActiveLearner be used for active regression using Gaussian processes. Since Gaussian processes provide a way to quantify uncertainty of the predictions as the covariance function of the process, they can be used in an active learning setting.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel, RBF
from modAL.models import ActiveLearner

%matplotlib inline

The dataset

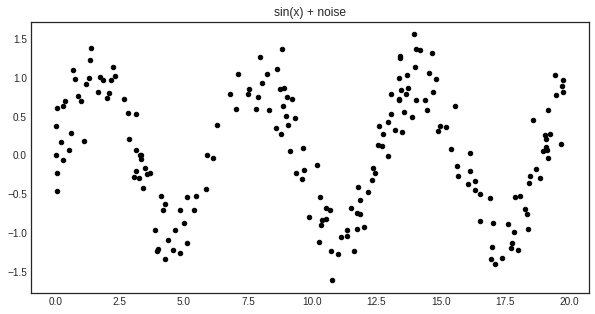
For this example, we shall try to learn the noisy sine function:

X = np.random.choice(np.linspace(0, 20, 10000), size=200, replace=False).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.3, size=X.shape)

with plt.style.context('seaborn-white'):
    plt.figure(figsize=(10, 5))
    plt.scatter(X, y, c='k', s=20)
    plt.title('sin(x) + noise')
    plt.show()

Uncertainty measure and query strategy for Gaussian processes

For active learning, we shall define a custom query strategy tailored to Gaussian processes. More information on how to write your custom query strategies can be found at the page Extending modAL. In a nutshell, a query stategy in modAL is a function taking (at least) two arguments (an estimator object and a pool of examples), outputting the index of the queried instance and the instance itself. In our case, the arguments are regressor and X.

def GP_regression_std(regressor, X):
    _, std = regressor.predict(X, return_std=True)
    query_idx = np.argmax(std)
    return query_idx, X[query_idx]

Active learning

Initializing the active learner is as simple as always.

n_initial = 5
initial_idx = np.random.choice(range(len(X)), size=n_initial, replace=False)
X_training, y_training = X[initial_idx], y[initial_idx]

kernel = RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e3)) \
         + WhiteKernel(noise_level=1, noise_level_bounds=(1e-10, 1e+1))

regressor = ActiveLearner(
    estimator=GaussianProcessRegressor(kernel=kernel),
    query_strategy=GP_regression_std,
    X_training=X_training.reshape(-1, 1), y_training=y_training.reshape(-1, 1)
)

The initial regressor is not very accurate.

X_grid = np.linspace(0, 20, 1000)
y_pred, y_std = regressor.predict(X_grid.reshape(-1, 1), return_std=True)
y_pred, y_std = y_pred.ravel(), y_std.ravel()

with plt.style.context('seaborn-white'):
    plt.figure(figsize=(10, 5))
    plt.plot(X_grid, y_pred)
    plt.fill_between(X_grid, y_pred - y_std, y_pred + y_std, alpha=0.2)
    plt.scatter(X, y, c='k', s=20)
    plt.title('Initial prediction')
    plt.show()

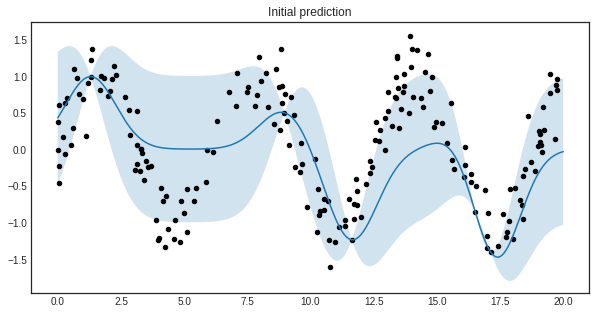
The blue band enveloping the regressor represents the standard deviation of the Gaussian process at the given point. Now we are ready to do active learning!

n_queries = 10
for idx in range(n_queries):
    query_idx, query_instance = regressor.query(X)
    regressor.teach(X[query_idx].reshape(1, -1), y[query_idx].reshape(1, -1))

y_pred_final, y_std_final = regressor.predict(X_grid.reshape(-1, 1), return_std=True)
y_pred_final, y_std_final = y_pred_final.ravel(), y_std_final.ravel()

with plt.style.context('seaborn-white'):
    plt.figure(figsize=(10, 8))
    plt.plot(X_grid, y_pred_final)
    plt.fill_between(X_grid, y_pred_final - y_std_final, y_pred_final + y_std_final, alpha=0.2)
    plt.scatter(X, y, c='k', s=20)
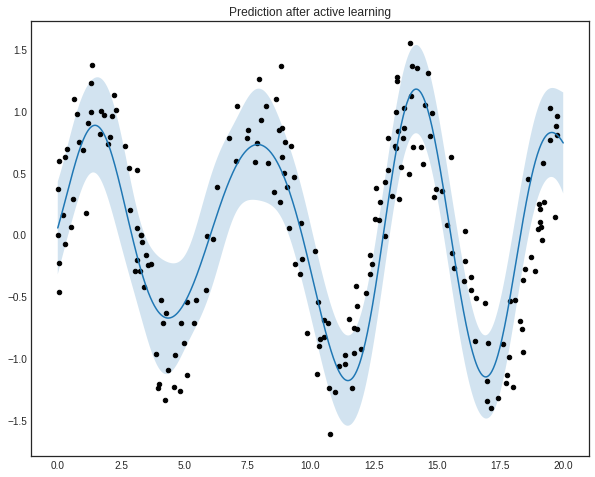
    plt.title('Prediction after active learning')
    plt.show()